Back in 2009 I had developed a tennis betting system based on rankings. I had used a mathematical formula I found in a publication of 2002. The calculations weren’t difficult and back testing the system using a sample of 600 tennis matches in an Excel spreadsheet proved worthwhile. Apparently though, I must have done that back testing in a bit of a hurry, as there were a couple of mistakes in the conclusions and graphs. I was reminded of that tennis betting system by John S. who sent me an email, wondering why I was worried of placing lay bets at big odds and didn’t omit those specific bets. So, I revisited the betting system this morning finding out that the system is profitable only if bettors lay at short odds – like a bookmaker does – or bet at bigger than average odds. No surprise there I suppose!
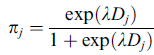
The formula that Klaassen and Magnus included in their publication and was the basis of my tennis betting system uses the tennis ranking system and introduces a constant, λ, which is 0.3986 in men’s singles and 0.715 in women’s singles. The spreadsheet I created calculated the probability of each tennis player to win each game and depending on the average odds found in the database, it was able to prompt the value bets I needed to risk my money on. Initially though, my back testing conclusion was that the system was profitable only if bettors bet against those value bets. In other words trying to turn a losing system into a winning one, since if one bet on the value bets, they would lose in the long run.
In that old post, I have published a rather impressive graph towards the article’s end, giving high hopes of the system’s profitability. On the other hand, due to having developed the system quickly, I assumed layers would have a steady profit target, risking different amounts per bet. While they stood to win 10 euros in each match, if they laid at 10.0 odds, they would risk 100 euros! That contradicts the flat betting system I always recommend of when back testing a new idea in gambling. We should always aim to risk the same amount of amount, instead of targeting the same profit out of each bet.
Today I spent some time on that excel spreadsheet, corrected the mistakes and found out that if one risks 10 units per lay bet, they will make some money in women’s matches but will break even in men’s matches. I used once again the sample of that old spreadsheet, meaning I had 600 Australian Open games to work with. I noticed though that the tennis betting system performed much better in WTA matches and that led me to download all 2010 and 2011 WTA games’ details. The database now consists of 5,000 women’s single matches taken place all over the world during 2010 and 2011. The results were astonishing as the forecasting formula calculated value bets of 6.1% +EV!
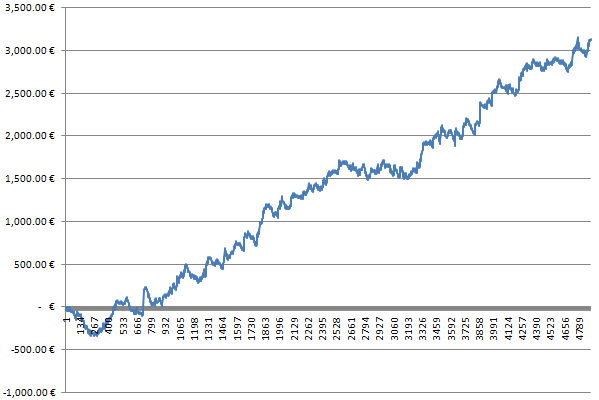
Ok, been there, done that a million times and by the end of the day I always find a minor detail I have skipped or a small calculations’ mistake I didn’t pay attention of. This time the betting system was profitable due to laying at short odds. The tennis database of tennis-data.co.uk includes the average odds of popular bookmakers. Therefore I had been placing lay bets at bookmakers’ short odds, comparing to a betting exchange. Although I included 5% commission in the calculations, the profit was still quite exceptional. Since I wouldn’t be able to lay at those odds, I had to try and back the opponent’s odds and find out how the system would perform.
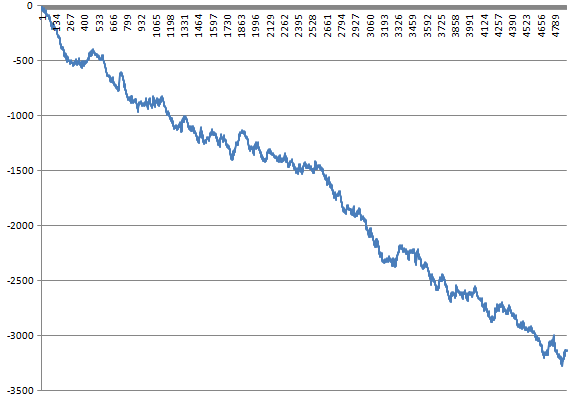
Obviously the results were disappointing, as I was now backing at somewhat short odds, again comparing to a betting exchange. I was now losing 6% of my money in each bet, resulting to a loss equal with the profit I made earlier. Some can say that the mirrored graphs prove the market’s efficiency in tennis matches. If we laid at bookmakers’ average odds we would win but would break even at a bit higher odds. If we backed at bookmakers’ average odds we would lose, but again break even at a bit higher odds. The market seems to be efficient enough and drive the odds close to the true probability. From that point on, bookmakers adding their vigorish eliminate much of the value punters could find in a zero-sum game. At least that is the case with the specific tennis system.
Maybe I will spend some more time comparing bookmakers’ odds with Betfair’s ones, but I don’t expect the system to have a better ROI of 3% or so in the best scenario. Unless the betting exchange’s odds are much closer to the ones of bookmakers, but I highly doubt it.